C Programming, P24

c程序：

 

?
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
#include <stdio.h>
#define CENTER 2
#define MARGIN 5
 
void star(line){
    int left, right, i;
    char ret[CENTER+MARGIN+1];
    for (i=0; i < CENTER+MARGIN+1; ++i)
        {
            ret[i]=' ';
        }
    if (line > MARGIN){
        return;
    }
 
    left = CENTER - MARGIN + line;
    right= CENTER + MARGIN - line;
    for (i=0; i <= right; i++){
        if (i==left || i==right){
            ret[i]='*';
        }
        else{
            ret[i]=' ';
        }
    }
    printf("%s\n", ret);
}
 
int main(void){
    int i;
    for (i = 0; i< 8; ++i)
    {
        star(i);
    }
}

输出：

 

?
1
2
3
4
5
6
       *
      *
     * 
*   *  
 * *   
  *

离散数学 c Comments(328) 12 years ago

c语言扑克洗牌

重新写的程序。每次洗出一张，放在最后，剩下的牌重新洗，直至最后一张。代码如下：

 

?
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
#include<stdio.h>
#include<time.h>
int N=54;
char * pk[]={"黑桃A","黑桃2","黑桃3","黑桃4","黑桃5","黑桃6","黑桃7","黑桃8","黑桃9","黑桃10","黑桃J","黑桃Q","黑桃K","红桃A","红桃2","红桃3","红桃4","红桃5","红桃6","红桃7","红桃8","红桃9","红桃10","红桃J","红桃Q","红桃K","草花A","草花2","草花3","草花4","草花5","草花6","草花7","草花8","草花9","草花10","草花J","草花Q","草花K","方块A","方块2","方块3","方块4","方块5","方块6","方块7","方块8","方块9","方块10","方块J","方块Q","方块K","大王","小王"};
main()
{
    int a[N];
 
    int i;
    int temp;
    int p;
    int ten=0;
    unsigned int time1,time2;
    int m=0;
    for (i=0;i<N;i++)
    {
        a[i]=i;
    }
 
    srand((unsigned)time(NULL));
    for (m=0;m<100000;m++){
    for (i=N-1;i>0;i--)
    {      
        temp= rand() % i;
        p=a[i];
        a[i]=a[temp];
        a[temp]=p;
    }}
 
    for (i=0;i<N;i++)
    {
        printf("%02d:%-5s  ",i+1,pk[a[i]]);
        ten++;
        if (ten==10)
        {
            printf("\n");
            ten=0;
        }
    }
    printf("\n");
 
}

 

 

贴图：

c语言扑克洗牌算法

算法笔记 算法 笔记 c Comments(1003) 16 years ago

c语言之洗牌算法

在火车上看人打扑克，想做个洗牌算法。我的思路用c语言实现，是这样的：

 

?
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
/*本程序是洗牌算法的c语言实现.
原理是,生成52个随机数;每生成一个,记录在数组中,同时记下该数已经生成.下次再生成随机数,如果
已经成生过,则重新生成一个随机数.生成与否,该信息记录在另一个数组中.例如,如果数字15已经成生,则
array[15]=1;
 
*/
 
#include<stdio.h>
#include<time.h>
#include<stdlib.h>
#define  N 52
int poker[N];   //用来记录生成的扑克代码
int back[N];    //用来记录"hash"信息
 
init_back()
{
//初始化hash数组
    int i=0;
    for (i=0;i<N;i++)
    {
        back[i]=0;
    }
     
}
 
//辅助函数,用来打印数组,每10个一行.
print_array(int * array)
{
    int i=0,m=0;
     
    for (i=0;i<N;i++)
    {      
        printf("%d ",array[i]);
        if ((i+1) % 10 ==0 && i)
        {
            printf("\n");
        }
    }  
    printf("\n"); 
}
 
//生成随机数.
rand_back()
{
    int i=0;
    int counter=0;                      //用来测试一共生成了多少次随机数.计算效率.
    srand((unsigned)time(   NULL   )   );//用来初始化随机函数,以便生成不同的随机数.
    for (i=0;i<N;i++)
    {
        ++counter;
        int p=rand()%N;
        if (!back[p])
        {
            poker[i]=p;
            back[p]=1;
        }
        else
        {
        i--;       
        }      
    }
    printf("the counter is: %d\t,效率是 %f;\n",counter,(52.0/counter));
     
}
 
int main()
{
    //print_array(poker);
    init_back();
    rand_back();
    //print_array(poker);
    //getchar();
 
}

生成其中一组随机记录为：

23 8 5 17 48 51 14 49 35 36
38 30 31 24 29 47 34 18 41 11
27 16 26 9 45 43 46 0 3 19
37 13 32 20 6 22 4 33 7 21
40 50 42 1 2 28 39 15 25 12
10 44

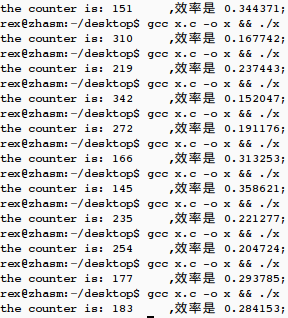
不过效率似乎不高。计算所生成的有效随机数与尝试次数之比，结果如下：

c语言之洗牌算法

算法笔记 c 算法 Comments(224) 16 years ago

逻辑联接词之合取

c语言提供了几个位操作符，其中：

  • bitwise AND operator: &
  • bitwise Exclusive OR operator: ^
  • bitwise Inclusive OR operator: |

其结合力是依次递减的。

清华版《离散数学》(9787302130666)，第1.2.2的合取、析取，使用c语言实现是：

?
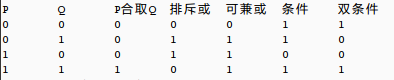
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
#include<stdio.h>
 
 
//条件：设p与q是两个命题，若p则q
//只有当p为1，q为0时返回0值，其余返回1.
tiaojian(p,q)
{
    return (p && !q)?0:1;
}
 
//双条件：设p与q是两个命题，p当且仅当q，p的充分必要条件是q
//当且仅当p与q同为0或同为1时返回1，其余返回0
shuangtiaojian(p,q)
{
    return ((p && q)||(!p && !q))?1:0;
}
 
main()
{
    int p,q;
    printf("P\tQ\tP合取Q\t排斥或\t可兼或\t条件\t双条件\n");
    for(p=0;p<=1;p++)
    {
        for(q=0;q<=1;q++)
        {
            printf("%d\t%d\t%d\t%d\t%d\t%d\t%d\n",p,q,p&q,p^q,p|q,tiaojian(p,q),shuangtiaojian(p,q));
        }
        //printf("\n");
    }
}

 

输出结果：

 

 

离散数学 c 离散数学 笔记 逻辑 Comments(302) 16 years ago

紫龙书3.4.5之KMP算法fail函数

我读的紫龙书是机械工业出版社2009.01之第2版。ISBN：978-7-111-25121-7。译者是南京大学的赵建华，邓滔，戴新宇。

该书74页有个错误：

3)串s的子串(substring)是删除s的某个前缀和某个后缀之后得到的串。例如，bnana，nan和e是bnana的子串。

第一感觉这里有问题。翻开英文原书，这样写的：

3. A substring of s is obtained by deleting any prefix and any suffix from s. For instance, banana, nan, and E are substrings of banana.

就应该只是删除子串嘛，不应该是删除0个或多个符号，成为子序列那样。本书的编辑真该打屁股。

另，3.4.5，

该函数的目标是使得b1b2...bf(s)是最长的既是b1b2...bn的真前缀又是b1b2...bs的后缀的子串。

对应英文是：

The objective is that blb2...bf(s) is the longest proper prefix of b1b2...bs, that is also a suffix of b1b2bs.

读过原文之后，才勉强可理解中文翻译。中文之所以费解，是由于将“最长的”三字依英文位置给前置了。私以为放在后面会好理解一些，如：

该函数的目标是使得b1b2...bf(s)既是b1b2...bn的真前缀又是b1b2...bs的后缀的最长的子串。

就此打住，切入正题。说一下失效函数。

原书中，图3－19给出的fail函数，我使用c语言做出来了。要点是原图中的下标是以1-based，翻译为c语言要调整为0-based。程序如下：

 

?
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
#include<stdio.h>
#include<string.h>
 
int fail(const char *b)
{
    int n=strlen(b);
    int t=0;
    int f[n+1];
    f[1]=0;
    int s;
    for(s=1;s<=n;s++)
    {
        while(t>0 && b[s]!= b[t])
        {
            t=f[t];
        }
        if (b[s]==b[t])
        {
            t++;
            f[s+1]=t;
        }
        else
        {
            f[s+1]=0;
        }
    }
    for (s=1;s<=n;s++)
    {
        printf("%d ",f[s]);
    }
    printf("\n");
}
 
main()
{
   fail("abababaab");
     
}

运行该程序，解得3.4.3各串的失效函数分别为：

  1. abababaab->0 0 1 2 3 4 5 1 2
  2. aaaaaa->0 1 2 3 4 5
  3. abbaabb->0 0 0 1 1 2 3

 

龙书笔记 c 龙书 笔记 Comments(1061) 16 years ago

中缀表达式转后缀表达式

最近在看龙书第1版。第二版的例子有的是以java写的。个人喜欢第一版的c程序。

看到第2.6，上面提供了一个中缀转后缀的C语言程序。不过只支持个位数，加减运算。我修改一下，使之增加对多位正整数、乘、除、小括号的支持。允许数字与操作符之间出现任意空白字​符。

理论依据很清晰，就不再写额外的注释了。

?
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
#include<stdio.h>
#include<ctype.h>
 
/*
中缀表达式
 
理论依据：
expr -> expr + term | expr - term | term
term -> term * factor | term / factor | factor
factor -> digit | ( expr )
 
*/
 
int la; //lookahead
 
 
main()
{
    la=getchar();       
    expr();
    putchar('\n');
}
 
is_space(c)
    int c;
{
    if (c==' ' || c=='\t')
    {
        return 1;
    }
    else return 0;
}
 
space()
{
    while (la==' ' || la=='\t')
    {
        la=getchar();
    }
}
 
expr()
{
    term();
    while(1)
    {
        if (la=='+')
        {
            putchar(' ');
            match('+');term();putchar(' ');putchar('+');
        }
        else if (la=='-')
        {
            putchar(' ');           
            match('-');term();putchar(' ');putchar('-');
        }
        /*
        else if (is_space(la))
        {
            space();
        }
        */
        else break;
    }
}
 
term()
{
    factor();
    while(1)
    {
        if (la=='*')
        {
            putchar(' ');
            match('*');factor();putchar(' ');putchar('*');
        }
        else if (la=='/')
        {
            putchar(' ');
            match('/');factor();putchar(' ');putchar('/');
        }
        /*
        else if (is_space(la))
        {
            space();
        }
        */
        else break;
    }
}
 
factor()
{
    space();
    if (isdigit(la))
    {
        while (isdigit(la))
        {
            putchar(la);
            match(la);
        }   
    }
    else if (la=='(')
    {
        while(la!=')')
        {
            la=getchar();
            expr();
        }
        la=getchar();       
    }
    space();
}
 
match(t)
int t;
{
    if (la==t)
    {
        la=getchar();
    }
    else error();
}
 
error()
{
    printf("syntax error\n");
}

 

 

龙书笔记 c 龙书 Comments(2953) 16 years ago